Implement Key Value Storage in C

Key Value Storage is an assignment of CSIE3006 - Operating System by Hung-Chang Hsiao at National Cheng Kung University. In this assignment, I made a single-threaded key value storage in C++. In this assignment, I referenced famous key-value storage projects such as LevelDB and other search and storage algorithms, and utilized Bloom filter, skip list, sorted string tables (SSTable), and binary search to enhance the speed of database searches. As a result, I achieved the second-highest grade in this assignment.

Now, I am rewriting this assignment in object-oriented techniques in C, ensuring clean code and adhering to SOLID principles. There are still a few memory leaks detected in this program, and I am currently working on fixing them.

GitHub repository: https://github.com/blueskyson/key-value-storage

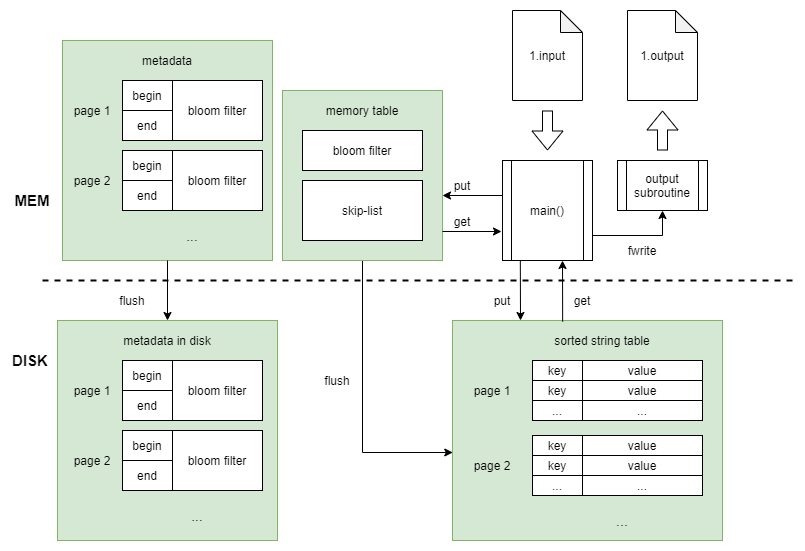
Program Development: Modules

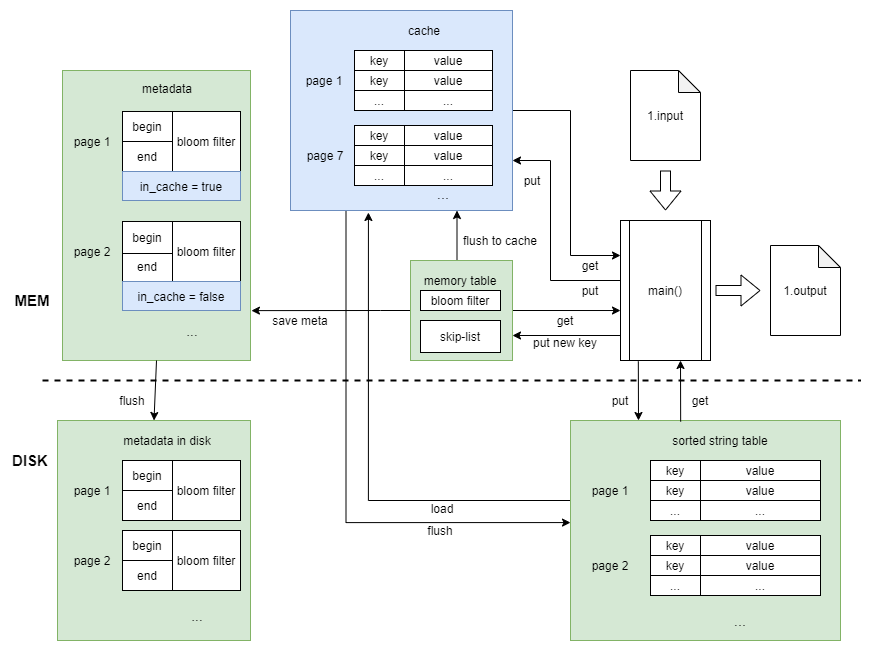
The diagram above shows the program architecture. Below is an introduction to each data structure:

• Bloom Filter
  The purpose of the bloom filter is to quickly verify whether a specified key exists in the skip list or SSTable (referred to as “page” in the code) before performing a search within the skip list or SSTable. It consists of a string with a length of 131,072 bytes. It references the jserv’s dict bloom filter implementation, using djb2 and Jenkins as hash functions. When recording 100,000 keys, the false positive rate is about 3%.
• Skip List
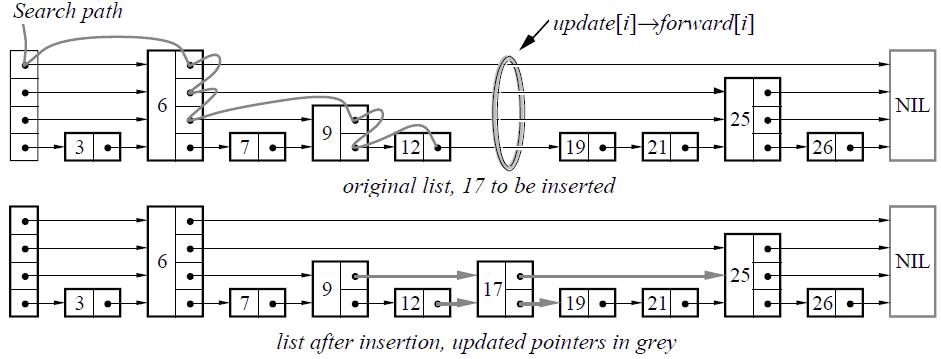
  A 4-level linked list where each node’s level is random. Pointers of the same level only point to the next node with a level greater than or equal to their own, and the keys are sorted in ascending order. When searching for a key, the search starts from the highest level and moves downward. The complexity is $O(logn)$. Below is a diagram illustrating element insertion.
• Sorted String Table (SSTable)
  It is flushed from the skip-list to the hard drive, where the key-value pairs are ordered by key size. Each key-value pair is 136 bytes (8-byte unsigned long long key and 128-byte char array value), allowing direct use of binary search to find keys and read/write corresponding values in the file. Each SSTable (page) can have up to 100,000 key-value pairs. Once it is filled with 100,000 key-value pairs, the keys are no longer modified.
• Metadata
  It mainly records the bloom filters and the head and tail key values of each SSTable. This information helps the program quickly determine whether to search a particular file (page). When the program starts, it loads all metadata into memory, and when the program ends, it writes the updated metadata back to the hard drive.

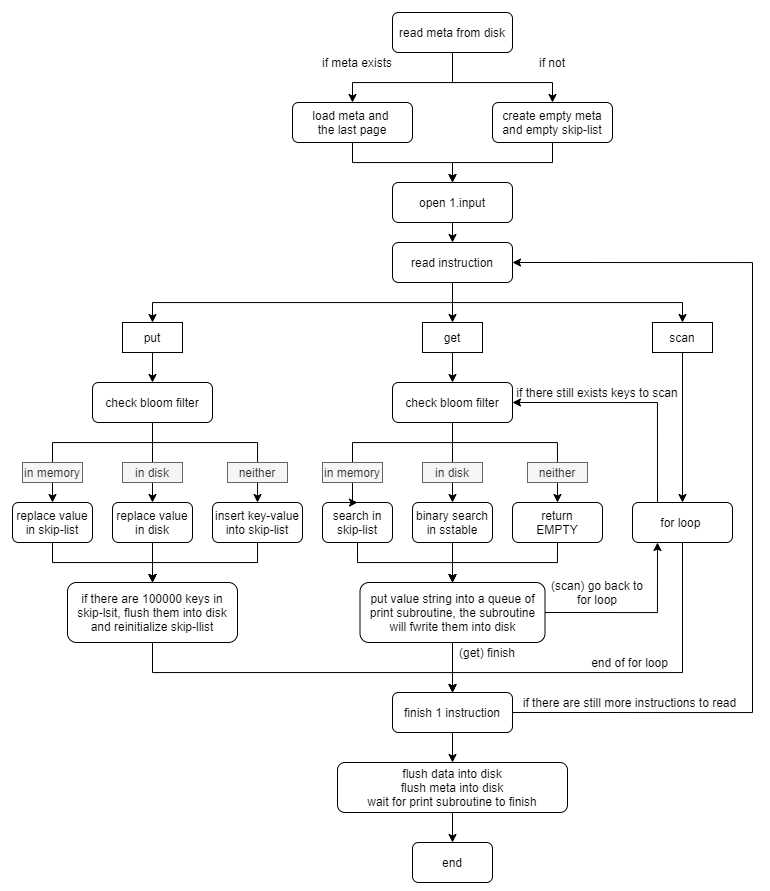
Program Development: Flow

When the program starts, it first checks the storage directory for metadata. If found, it indicates that the database already contains data, so the metadata is read into memory, and the page with the highest number is loaded into memory as a skip list. If not found, it generates empty metadata and a skip-list.

Next, it opens text file 1.input to read commands:

• PUT: It first searches for the key in the skip list, then compares the Bloom filters of each SSTable one by one. If a Bloom filter indicates that the key exists, it searches the SSTable. Since the SSTable store key-value pair by accending order, I can uses mmap to open entire SSTable and use binary search to find the key. At most, it needs to search $log_2100000 = 17$ times to find the key and overwrite the value. If the key is not found, it adds a new node to the skip list to store the key-value pair. After completing the put operation, if the number of nodes in the skip list reaches 100,000, the skip list is flushed to the hard drive, becoming a new SSTable, and its metadata is added to the metadata list.
• GET: The search method is identical to put, but it does not overwrite the SSTable or add nodes. After the search, the resulting string is added to the tail of the print subroutine’s deque, which is responsible for writing to 1.output. The print subroutine continuously reads strings from the deque’s head, outputs them, and releases them.

Last, repeat until all commands are read. After reading all commands, the new metadata is written over the metadata on the hard drive, the skip-list is saved as the last page.

Performance Analysis

Analysis 1: Time for PUT Operations

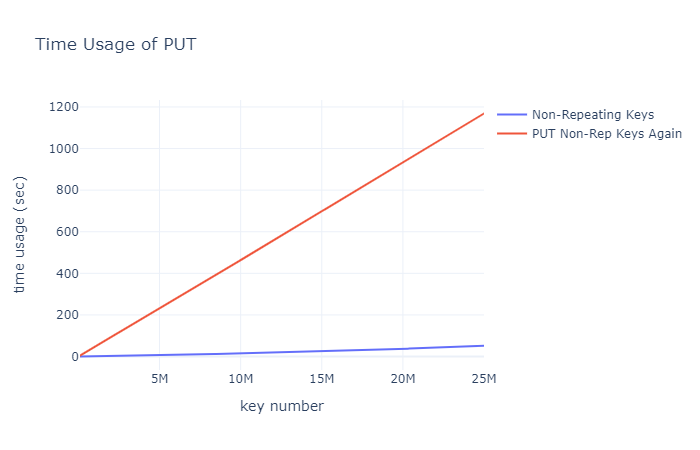
First, we analyze the time taken for continuously putting 25 million unique keys (using 0 - 24999999 for the experiment). The test method involves generating an input file with 25 million PUT commands, each with a unique key. Time is recorded after every 100,000 key-value pairs are put. The testing hardware includes an i7-10750H CPU and an M.2 SSD. Putting 25 million non-repeating keys took a total of 51 seconds, with an average of 0.204 seconds per 100,000 key-value pairs. The time taken for PUT operations closely follows a linear function, as shown by the blue line in the chart below.

Next, the same input file is fed to the database again. Since the key-value pairs were already stored on the hard drive during the previous experiment, this time the experiment doesn’t consume additional storage space but uses binary search to find the same keys in the SSTable and overwrite the values on the hard drive. Putting 25 million keys took a total of 1180 seconds, with an average of 4.7 seconds per 100,000 key-value pairs. The time taken for PUT operations closely follows a linear function, as shown by the red line in the chart below.

If the keys are random, the time consumed should fall between the red and blue lines.

This shows that in the current implementation, PUT operations for existing keys are faster than PUT operations for new keys.

Analysis 2: Time for GET Operations

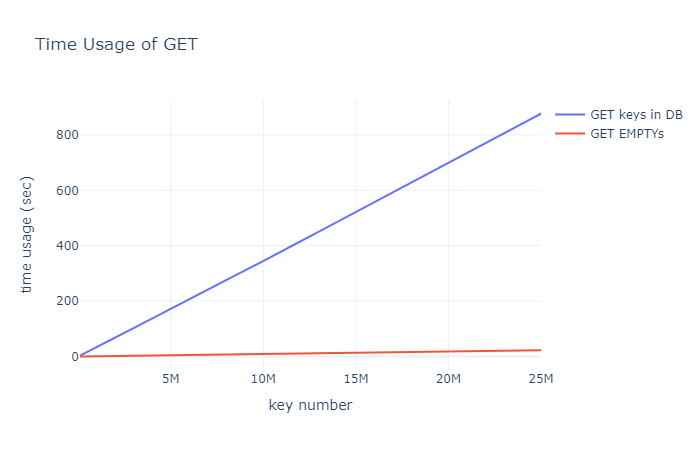
sing the same database from the previous PUT experiment, we first GET each key in the database (0 - 24999999). The time taken is shown by the blue line in the chart below, with a total of 877.194100 seconds, averaging 3.5 seconds per 100,000 keys.

Next, we GET 25 million keys that do not exist in the database. The time taken is shown by the red line in the chart below, with a total of 22.762612 seconds, averaging 0.09 seconds per 100,000 keys. This rapid performance is likely due to the bloom filter quickly filtering out non-existent keys in $O(1)$.

The bloom filter significantly accelerates the search time for non-existent keys.

Analysis 3: Disk Space Usage

Each SSTable typically stores 100,000 key-value pairs and is accompanied by metadata. The metadata records the first and last key values of the SSTable, the number of keys (int), and a bloom filter. Assuming there are $N$ key-value pairs, we can calculate the disk space usage of the database:

• Each key is 8 bytes unsigned long long, and each value is 128 bytes char array, so the SSTable will consume $N \times 136$ bytes.
• The metadata consists of 16 bytes for the first and last keys, 4 bytes for the key count, and 131,072 bytes for the bloom filter. Since metadata is added for every 100,000 keys, the space used by metadata is $(\lfloor N/100000 \rfloor + 1)*131092$ bytes
• The total disk space usage is the sum of the SSTable and metadata.

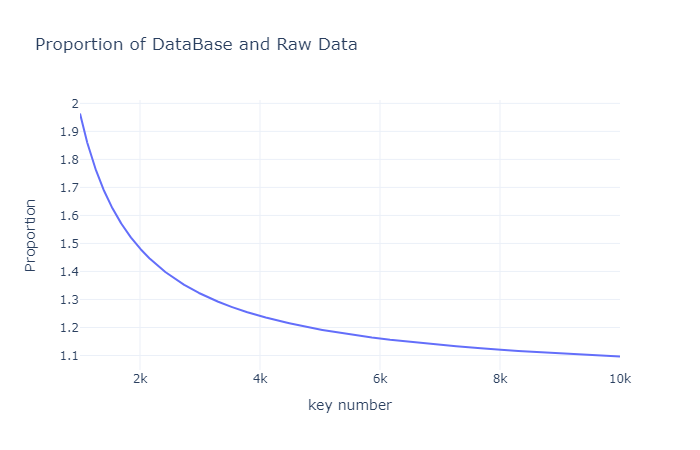
In summary, storing fewer key-value pairs in the database can be relatively inefficient due to the large space occupied by the bloom filter in the metadata. Conversely, storing a large number of key-value pairs can slightly reduce the percentage of space taken up by the metadata.

For every 13.6 MB (100,000 key-value pairs) added, an additional 131.092 KB of metadata is required. The ratio is $(13.6 MB + 131.092 KB) / 13.6 MB \approx 1.0096,$ resulting in approximately a 0.9% increase in size compared to the original data. As shown in the chart below, the more keys stored, the smaller the ratio of the database size to the original data size.

Storing more key-value pairs is more efficient in terms of disk space usage.

Analysis 4: Skip List Performance

The sparsity of nodes at different levels in the skip list is crucial for search efficiency. After numerous adjustments to the probability of generating new nodes at various levels, I settled on the probabilities: level 1 is generated with a probability of 1, level 2 with 1/16, level 3 with 1/128, and level 4 with 1/2048.

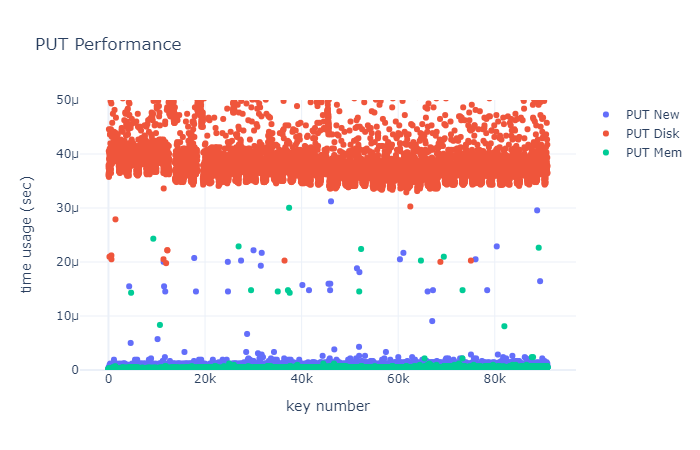
I further analyzed the time consumed by a single PUT operation and categorized PUT into three types:

• PUT New: The key-value pair is neither in the skip list nor in the SSTable.
• PUT Disk: The key-value pair is in the SSTable.
• PUT Mem: The key-value pair is in the skip list.

I tested each of these three types of PUT operations 100,000 times, recording the latency for each PUT command:

From the chart, it can be observed that the time consumed by skip list operations, aside from some outliers, is almost always less than 1 microsecond (the Y-axis in the chart is not precise enough to show this). PUT New is slightly slower than PUT Mem because it requires allocating a new node; meanwhile, PUT Disk’s time consumption ranges between 35 and 100 microseconds. Both PUT New and PUT Mem are significantly faster than PUT Disk.

Optimizing Program Modules

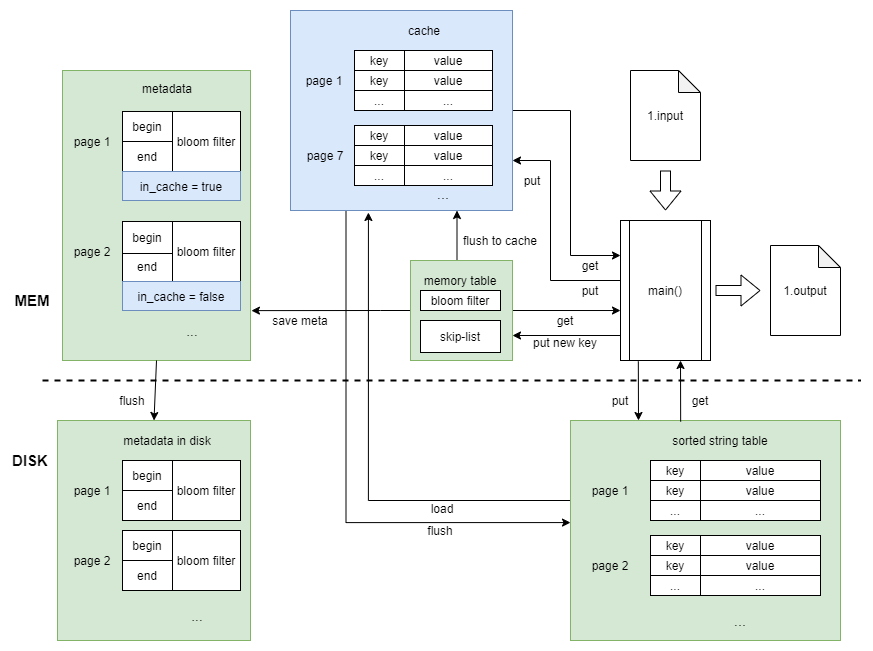
Although in-memory search performance has improved by Bloom filter and skip list significantly, the program uses too little memory. At most, fewer than 100,000 key-value pairs are kept in the in-memory skip-list, which amounts to 13.6 MB of data.

Typically, after accounting for the assessment environment, there is at least 2.5 GB of memory available. Using only 13.6 MB is quite conservative. To enhance memory usage efficiency, I made some modifications to the program architecture as follows:

I defined a new object called Cache that can store and manage SSTables. Additionally, I added a boolean value, in_cache, to the metadata to indicate whether a page is present in the cache. Whenever a PUT or GET operation accesses a page on the hard drive, I load that page into the cache. This way, future accesses to the same page do not require searching the hard drive again. When the number of pages in the cache reaches its limit (I set it to 130 pages, or 13 million key-value pairs), I flush the first loaded page back to the hard drive.

Furthermore, I removed the print subroutine, as spawning a thread for output did not speed up the process and instead led to errors.

Still refactoring the code into C, TBD…