Fibdrv is a Linux kernel module that calculates the Fibonacci sequence. It is an assignment of CSIE3018 - Linux Kernel Internals by Ching-Chun (Jim) Huang at National Cheng Kung University. In this assignment, I made fibdrv theoretically possible to calculate $F_{188795}$ and, using the relationship between the Fibonacci sequence and the golden ratio, made memory allocation deterministic. Additionally, I used Fast Doubling to reduce the amount of computations, and compared the computation times of the Karatsuba and Schönhage–Strassen algorithms.
Programs usually use previous generated values as the basis for the next calculation when computing random numbers. See Pseudo-Random Number Generators (PRNG). Fibonacci, after modifying the initial value or performing mod calculations, can produce numbers that are not easily predictable. This method of generating random numbers is called Lagged Fibonacci generator (LFG). See also: For The Love of Computing: The Lagged Fibonacci Generator — Where Nature Meet Random Numbers.
The expected goals are:
- Writing programs for the Linux kernel level
- Learning core APIs such as
ktimerandcopy_to_user - Reviewing C language numerical systems and bitwise operations
- improving numerical analysis and computation strategies
- Exploring Linux VFS
- Implementing automatic testing mechanisms
- Conducting performance analysis through
perf
Homework instructions (in Chinese): https://hackmd.io/@sysprog/linux2022-fibdrv
GitHub repository: https://github.com/blueskyson/fibdrv
Replace long long with custome struct BigN
This is the initial function that calculate Fibonacci $F_{k}$ in fibdrv.c:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
static long long fib_sequence(long long k)
{
/* FIXME: C99 variable-length array (VLA) is not allowed in Linux kernel. */
long long f[k + 2];
f[0] = 0;
f[1] = 1;
for (int i = 2; i <= k; i++) {
f[i] = f[i - 1] + f[i - 2];
}
return f[k];
}
fib_sequence uses long long to process the value of Fibonacci sequence, and it will overflow when reaching $F_{93}$ , so long long must be replaced by a data structure that can store larger values. First define struct BigN in client.c and fibdrv.c and give it an type u128:
1
2
3
4
5
6
#define BIGN
#ifdef BIGN
typedef struct BigN {
unsigned long long upper, lower;
} u128;
#endif
Ensure that lower can store up to $10^{19}$ at most, so the value represented by u128 is $upper * 10^{19} + lower$. This way, the rules for carrying from lower to upper will be similar to carrying in base $10^{19}$, and the range of representable values will be from $0$ to $1.8 * 10^{38}$, following this pattern:
| decimal | upper | lower |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 2 | 0 | 2 |
| $10^{19} - 1$ | 0 | 99…99 |
| $10^{19}$ | 1 | 0 |
| $10^{19} + 1$ | 1 | 1 |
| $2 * 10^{19} - 1$ | 1 | 99…99 |
| $2 * 10^{19}$ | 2 | 0 |
This allows us to easily use printf to print the string as follows:
1
printf("%llu%019llu", fib->upper, fib->lower);
The fib_sequence rewritten using u128 is as follows:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#ifdef BIGN
#define P10_UINT64 10000000000000000000ULL
static u128 fib_sequence_u128(long long k)
{
if (k <= 1LL) {
u128 ret = {.upper = 0, .lower = (unsigned long long) k};
return ret;
}
u128 a, b, c;
a.upper = 0;
a.lower = 0;
b.upper = 0;
b.lower = 1;
for (int i = 2; i <= k; i++) {
c.lower = a.lower + b.lower;
c.upper = a.upper + b.upper;
// if the lower overflows or the lower >= 10^9, then add a carry to upper
if ((c.lower < a.lower) || (c.lower >= P10_UINT64)) {
c.lower -= P10_UINT64;
c.upper += 1;
}
a = b;
b = c;
}
return c;
}
#endif
Next, I will modify the interface (fib_read) that calls this kernel driver. The original fib_read function directly returns the value of $F_k$ to user space, which means it tells client.c the value of $F_k$ through the return value of read(fd, buf, 1), with the type being ssize_t. Referring to Integer-Types, I found that ssize_t on my machine is 64 bits. Obviously, passing values of $F_{93}$ or higher using ssize_t will cause an overflow. Therefore, I should use the copy_to_user API to copy the data of $F_k$ into the buf of read(fd, buf, 1), and perform base conversion in client.c. The modified fib_read is as follows:
1
2
3
4
5
6
7
8
9
10
11
12
13
static ssize_t fib_read(struct file *file,
char *buf,
size_t size,
loff_t *offset)
{
#ifdef BIGN
u128 fib = fib_sequence_u128(*offset);
copy_to_user(buf, &fib, sizeof(fib));
return sizeof(fib);
#else
return (ssize_t) fib_sequence(*offset);
#endif
}
Next, rewrite client.c to read value from fibdrv:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#define FIB_DEV "/dev/fibonacci"
#define BIGN
#ifdef BIGN
typedef struct BigN {
unsigned long long upper, lower;
} u128;
void print_fib_u128(int i, u128 *fib)
{
if (fib->upper) {
printf("Reading from " FIB_DEV
" at offset %d, returned the sequence "
"%llu%019llu.\n",
i, fib->upper, fib->lower);
} else {
printf("Reading from " FIB_DEV
" at offset %d, returned the sequence "
"%llu.\n",
i, fib->lower);
}
}
#endif
int main()
{
long long sz;
char buf[sizeof(u128)];
char write_buf[] = "testing writing";
int offset = 100; /* TODO: try test something bigger than the limit */
int fd = open(FIB_DEV, O_RDWR);
if (fd < 0) {
perror("Failed to open character device");
exit(1);
}
for (int i = 0; i <= offset; i++) {
sz = write(fd, write_buf, strlen(write_buf));
printf("Writing to " FIB_DEV ", returned the sequence %lld\n", sz);
}
for (int i = 0; i <= offset; i++) {
lseek(fd, i, SEEK_SET);
sz = read(fd, buf, sizeof(u128));
#ifdef BIGN
print_fib_u128(i, (u128 *) buf);
#else
printf("Reading from " FIB_DEV
" at offset %d, returned the sequence "
"%lld.\n",
i, sz);
#endif
}
for (int i = offset; i >= 0; i--) {
lseek(fd, i, SEEK_SET);
sz = read(fd, buf, sizeof(u128));
#ifdef BIGN
print_fib_u128(i, (u128 *) buf);
#else
printf("Reading from " FIB_DEV
" at offset %d, returned the sequence "
"%lld.\n",
i, sz);
#endif
}
close(fd);
return 0;
}
This BigN implementation can compute up to
The current implementation is commit 53f5ddf.
Extending struct BigN to Compute $F_{1000}$
Rewrite struct BigN and name it ubig, expanding upper and lower to cell[size] as follows:
1
2
3
4
5
6
7
8
9
10
11
12
#define BIGN
#ifdef BIGN
#define BIGNSIZE 12
typedef struct BigN {
unsigned long long cell[BIGNSIZE];
} ubig;
#define init_ubig(x) for (int i = 0; i < BIGNSIZE; x.cell[i++] = 0)
#endif
The macro BIGNSIZE is used to control the length of the cell array. When BIGNSIZE is set to 12, ubig becomes a cell with 768 bits to store Fibonacci sequence values, capable of representing numbers from $0$ to $1.8 * 10^{19 * 12}$. cell[0] stores the least significant bits, and cell[11] stores the most significant bits. Next, rewrite fib_sequence:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#ifdef BIGN
#define P10_UINT64 10000000000000000000ULL
static ubig fib_sequence_ubig(long long k)
{
if (k <= 1LL) {
ubig ret;
init_ubig(ret);
ret.cell[0] = (unsigned long long) k;
return ret;
}
ubig a, b, c;
init_ubig(a);
init_ubig(b);
b.cell[0] = 1;
for (int i = 2; i <= k; i++) {
for (int j = 0; j < BIGNSIZE; j++)
c.cell[j] = a.cell[j] + b.cell[j];
for (int j = 0; j < BIGNSIZE - 1; j++) {
if ((c.cell[j] < a.cell[j]) || (c.cell[j] >= P10_UINT64)) {
c.cell[j] -= P10_UINT64;
c.cell[j + 1] += 1;
}
}
a = b;
b = c;
}
return c;
}
#endif
The current implementation is commit d0dd8a4.
Improving struct BigN
Currently, each unsigned long long in struct BigN will carry over when it reaches $10^{19}$, but when implementing the Fast Doubling algorithm, directly performing left shifts will lead to errors because upper and lower are not separated by $2^{64}$. Therefore, I simply let the cell array use unsigned binary representation, which is $upper * 2^{64} + lower$. The binary to Base-10 conversion will be done when printing to the terminal.
| decimal | upper | lower |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 2 | 0 | 2 |
| $2^{64}$ - 1 | 0 | 0xff…ff |
| $2^{64}$ | 1 | 0 |
| $2^{64} + 1$ | 1 | 1 |
| $2^{65} - 1$ | 1 | 0xff…ff |
| $2^{65}$ | 2 | 0 |
Here is the implementation of improved addition (ubig_add) after the enhancement:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#define BIGNSIZE 12
typedef struct BigN {
unsigned long long cell[BIGNSIZE];
} ubig;
static inline void init_ubig(ubig *x)
{
for (int i = 0; i < BIGNSIZE; x->cell[i++] = 0)
;
}
static inline void ubig_add(ubig *dest, ubig *a, ubig *b) {
for (int i = 0; i < BIGNSIZE; i++)
dest->cell[i] = a->cell[i] + b->cell[i];
for (int i = 0; i < BIGNSIZE - 1; i++)
dest->cell[i + 1] += (dest->cell[i] < a->cell[i]);
}
Next, let’s apply the ubig_add implementation to modify fibdrv:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
static ubig fib_sequence_ubig(long long k)
{
if (k <= 1LL) {
ubig ret;
init_ubig(&ret);
ret.cell[0] = (unsigned long long) k;
return ret;
}
ubig a, b, c;
init_ubig(&a);
init_ubig(&b);
b.cell[0] = 1ULL;
for (int i = 2; i <= k; i++) {
ubig_add(&c, &a, &b);
a = b;
b = c;
}
return c;
}
#define BUFFSIZE 500
static ssize_t fib_read(struct file *file,
char *buf,
size_t size,
loff_t *offset)
{
#ifdef BIGN
char fibbuf[BUFFSIZE];
ubig fib = fib_sequence_ubig(*offset);
int __offset = ubig_to_string(fibbuf, BUFFSIZE, &fib);
copy_to_user(buf, fibbuf + __offset, BUFFSIZE - __offset);
return (ssize_t) BUFFSIZE - __offset;
#else
return (ssize_t) fib_sequence(*offset);
#endif
}
The current implementation is commit b2749a6.
Computing Fibonacci Sequence using Fast Doubling
First, implement subtraction (ubig_sub), left shift (ubig_lshift), and long multiplication (ubig_mul) for struct BigN:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
static inline void ubig_sub(ubig *dest, ubig *a, ubig *b)
{
for (int i = 0; i < BIGNSIZE; i++)
dest->cell[i] = a->cell[i] - b->cell[i];
for (int i = 0; i < BIGNSIZE - 1; i++)
dest->cell[i + 1] -= (dest->cell[i] > a->cell[i]);
}
static inline void ubig_lshift(ubig *dest, ubig *a, int x)
{
init_ubig(dest);
// quotient and remainder of x being divided by 64
unsigned quotient = x >> 6, remainder = x & 0x3f;
for (int i = 0; i + quotient < BIGNSIZE; i++)
dest->cell[i + quotient] |= a->cell[i] << remainder;
if (remainder)
for (int i = 1; i + quotient < BIGNSIZE; i++)
dest->cell[i + quotient] |= a->cell[i - 1] >> (64 - remainder);
}
void ubig_mul(ubig *dest, ubig *a, ubig *b)
{
init_ubig(dest);
int index = BIGNSIZE - 1;
while (index >= 0 && !b->cell[index])
index--;
if (index == -1)
return;
for (int i = index; i >= 0; i--) {
int bit_index = (i << 6) + 63;
for (unsigned long long mask = 0x8000000000000000ULL; mask;
mask >>= 1) {
if (b->cell[i] & mask) {
ubig shift, tmp;
ubig_lshift(&shift, a, bit_index);
ubig_add(&tmp, dest, &shift);
*dest = tmp;
}
bit_index--;
}
}
}
Refer to the Fast Doubling algorithm:
\[\begin{split} \begin{bmatrix} F(2n+1) \\ F(2n) \end{bmatrix} &= \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}^{2n} \begin{bmatrix} F(1) \\ F(0) \end{bmatrix}\\ \\ &= \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}^n \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}^n \begin{bmatrix} F(1) \\ F(0) \end{bmatrix}\\ \\ &= \begin{bmatrix} F(n+1) & F(n) \\ F(n) & F(n-1) \end{bmatrix} \begin{bmatrix} F(n+1) & F(n) \\ F(n) & F(n-1) \end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix}\\ \\ &= \begin{bmatrix} F(n+1)^2 + F(n)^2\\ F(n)F(n+1) + F(n-1)F(n) \end{bmatrix} \end{split}\]Now we have:
\[\begin{split} F(2k) &= F(k)[2F(k+1) - F(k)] \\ F(2k+1) &= F(k+1)^2+F(k)^2 \end{split}\]Pseudo code:
1
2
3
4
5
6
7
8
9
10
Fast_Fib(n)
a = 0; b = 1; // m = 0
for i = (number of binary digit in n) to 1
t1 = a*(2*b - a);
t2 = b^2 + a^2;
a = t1; b = t2; // m *= 2
if (current binary digit == 1)
t1 = a + b; // m++
a = b; b = t1;
return a;
For example: Computing $F(10)$:
| i | start | 4 | 3 | 2 | 1 | result |
|---|---|---|---|---|---|---|
| n | - | 1010 | 1010 | 1010 | 1010 | - |
| F(m) | F(0) | F(0*2+1) | F(1*2) | F(2*2+1) | F(5*2) | F(10) |
| a | 0 | 1 | 1 | 5 | 55 | 55 |
| b | 1 | 1 | 2 | 8 | 89 | - |
Implementing fibdrv using Fast Doubling:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
static ubig fib_sequence_ubig(long long k)
{
if (k <= 1LL) {
ubig ret;
init_ubig(&ret);
ret.cell[0] = (unsigned long long) k;
return ret;
}
ubig a, b;
init_ubig(&a);
init_ubig(&b);
b.cell[0] = 1ULL;
for (unsigned long long mask = 0x8000000000000000ULL >> __builtin_clzll(k);
mask; mask >>= 1) {
ubig tmp1, tmp2, t1, t2;
ubig_lshift(&tmp1, &b, 1); // tmp1 = 2*b
ubig_sub(&tmp2, &tmp1, &a); // tmp2 = 2*b - a
ubig_mul(&t1, &a, &tmp2); // t1 = a*(2*b - a)
ubig_mul(&tmp1, &a, &a); // tmp1 = a^2
ubig_mul(&tmp2, &b, &b); // tmp2 = b^2
ubig_add(&t2, &tmp1, &tmp2); // t2 = a^2 + b^2
a = t1, b = t2;
if (k & mask) {
ubig_add(&t1, &a, &b); // t1 = a + b
a = b, b = t1;
}
}
return a;
}
The current implementation is commit 473ff4a.
Performance Analysis of Addition and Fast Doubling
Isolating Specific CPUs
1
2
3
4
5
6
7
8
9
10
$ lscpu
Architecture: x86_64
CPU op-mode(s): 32-bit, 64-bit
Byte Order: Little Endian
Address sizes: 39 bits physical, 48 bits virtual
CPU(s): 12
On-line CPU(s) list: 0-11
Thread(s) per core: 2
Core(s) per socket: 6
...
First, modify the GRUB configuration file to force isolate a CPU:
1
$ sudo vim /etc/default/grub
Edit GRUB_CMDLINE_LINUX="":
1
GRUB_CMDLINE_LINUX="isolcpus=0"
Update GRUB:
1
$ sudo update-grub
After rebooting, use taskset to check if the CPU has been isolated:
1
2
$ taskset -p 1
pid 1's current affinity mask: 7ff
Run the client program pinned to the isolated CPU:
1
2
$ sudo insmod fibdrv.ko
$ sudo taskset -c 11 ./client
Eliminating Other Interfering Factors
Disable address space layout randomization (ASLR):
1
$ sudo sh -c "echo 0 > /proc/sys/kernel/randomize_va_space"
Set the scaling_governor to “performance”:
1
2
3
4
5
# performance.sh
for i in /sys/devices/system/cpu/cpu*/cpufreq/scaling_governor
do
echo performance > ${i}
done
Disable turbo mode of Intel processors:
1
$ sudo sh -c "echo 1 > /sys/devices/system/cpu/intel_pstate/no_turbo"
Calculating Execution Time of fibdrv in Kernel Space
Use ktime_t and ktime_get() to handle the computation time of the Fibonacci sequence. Finally, pass the elapsed time to user space through the return value of fib_read. The specific implementation is as follows:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <linux/ktime.h>
// ...
static ssize_t fib_read(struct file *file,
char *buf,
size_t size,
loff_t *offset)
{
#ifdef BIGN
ktime_t t = ktime_get();
char fibbuf[BUFFSIZE];
ubig fib = fib_sequence_ubig(*offset);
int __offset = ubig_to_string(fibbuf, BUFFSIZE, &fib);
copy_to_user(buf, fibbuf + __offset, BUFFSIZE - __offset);
s64 elapsed = ktime_to_ns(ktime_sub(ktime_get(), t));
return elapsed;
#else
return (ssize_t) fib_sequence(*offset);
#endif
}
Then write a perf-test.c to print the execution time of user space, kernel space, and kernel to user. This program will repeatedly calculate $F_0$ to $F_{1000}$ 100 times and compute the 10% trimmed mean.
Next, Pipe the test results to fast_doubling.txt:
1
2
3
4
$ gcc perf-test.c -o a
$ sudo insmod fibdrv.ko
$ sudo taskset -c 11 ./a > fast_doubling.txt
$ sudo rmmod fibdrv.ko || true >/dev/null
The output results will be like:
1
2
3
4
5
6
0 232 543 311
1 51551 51835 284
2 52655 52997 342
3 52379 52663 284
4 52758 53041 283
...
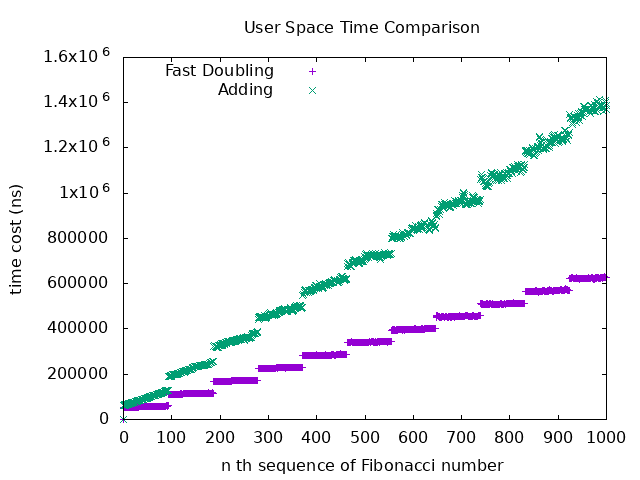
Compare the user space time of Fast Doubling and Adding:
It can be observed that Fast Doubling outperforms Adding in terms of performance.
The current implementation is commit 48956a1.
One-on-One Review with Professor on 2022/04/02
- Estimate the significant digits before calculating decimal values.
- Abstraction: Abstract the implementation to reduce redundant code modifications and increase readability.
- Determinism: Prepare memory allocation before starting the calculation. If memory allocation fails, return a failure message immediately to avoid wasting calculation time.
- Reduce the data transfer between kernel and user space.
When dynamically allocating memory, consider the following issues:
- Continuous unsigned long long may fail when dynamically allocated.
- Multiplication operation: m digits * m digits => results in 2m digits => memory allocation must be done in advance (cannot be done in-place).
- Binary to decimal conversion also requires dynamic memory allocation.
- During the kernel to user data transfer, it’s possible to encounter insufficient memory allocated by the client (user) beforehand.
Abstracting the Interface and Implementation
I have abstracted the functions for big number addition, multiplication, initialization, and others as follows:
1
2
3
4
5
6
7
8
9
10
11
12
13
// ubig_xxx.h
ubig *new_ubig(int size);
void destroy_ubig(ubig *ptr);
void zero_ubig(ubig *x);
void ubig_assign(ubig *dest, ubig *src);
void ubig_add(ubig *dest, ubig *a, ubig *b);
void ubig_sub(ubig *dest, ubig *a, ubig *b);
void ubig_lshift(ubig *dest, ubig *a, int x);
void ubig_mul(ubig *dest, ubig *a, ubig *b, ubig *shift_buf, ubig *add_buf);
int ubig_to_string(char *buf, size_t bufsize, ubig *a);
ubig fib_sequence(long long k);
Different versions of implementations are written in ubig_1.h, ubig_2.h, and so on. In fibdrv.c, different implementations are switched by #include "ubig_xxx.h".
Estimating the Significant Digits of $F_n$
According to relation to the golden ratio, the ratio of consecutive Fibonacci numbers approaches the golden ratio, which is $F_n * 1.61803… \approx F_{n+1}$.
Moreover, $\dfrac{1}{\log_{10}\ 1.61804} \approx 4.78518$, which means that when the ratio of consecutive Fibonacci numbers approaches 1.61804, in decimal representation, every increase of four to five terms will result in an additional digit.
Let’s list some Fibonacci numbers and observe at which point $\dfrac{F_{k}}{F_{k-1}}$ becomes less than $1.61804$:
| $k$ | $F_k$ | $F_k/F_{k-1}$ |
|---|---|---|
| 13 | 233 | 1.6180555556 |
| 14 | 377 | 1.6180257511 |
| 15 | 610 | 1.6180371353 |
| 16 | 987 | 1.6180327869 |
| 17 | 1597 | 1.6180344478 |
From the listing, we can see that when $k \geq 14$, $\dfrac{F_k}{F_{k-1}}$ converges to less than 1.61804. Therefore, when $k \geq 14$, we can estimate the decimal digits of $F_k$ using $\lfloor log_{10}\ 233+(k-13)log_{10}\ 1.61804 \rfloor + 1$. This equation can be simplified to $\lfloor k0.20899 + 0.6505 \rfloor$.
Assuming ubig uses $N$ unsigned long long numbers, computing $\left\lfloor \dfrac{\log_2 \ 2^{64N}}{\log_2 \ 10} \right\rfloor + 1$ gives the maximum number of digits ubig can represent. Simplifying the constants, this becomes $\lfloor N*19.26593 + 1\rfloor$.
We can dynamically adjust the value of $N$ based on the value of $k$ by ensuring $\lfloor N19.2661 + 1\rfloor \geq \lfloor k0.20899 + 0.6505 \rfloor$. Below is the function to estimate the required number of unsigned long long numbers (since kernel modules do not allow floating-point arithmetic, the pre-computed constants are multiplied by 100000 and then used for integer calculations):
1
2
3
4
5
6
static inline int estimate_size(long long k) {
if (k <= 93)
return 1;
unsigned long long n = (k * 20899 - 34950) / 1926610;
return (int)n + 1;
}
Next, rewrite the ubig to allow adjusting the length of the unsigned long long array as needed.
1
2
3
4
typedef struct BigN {
int size;
unsigned long long *cell;
} ubig;
Allocate memory for ubig using kmalloc and release memory using kfree:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
ubig *new_ubig(int size)
{
ubig *ptr = kmalloc(sizeof(ubig), GFP_KERNEL);
if (!ptr)
return NULL;
unsigned long long *ullptr =
kmalloc(size * sizeof(unsigned long long), GFP_KERNEL);
if (!ullptr) {
kfree(ptr);
return NULL;
}
memset(ullptr, 0, size * sizeof(unsigned long long));
ptr->size = size;
ptr->cell = ullptr;
return ptr;
}
static inline void destroy_ubig(ubig *ptr)
{
if (ptr) {
if (ptr->cell)
kfree(ptr->cell);
kfree(ptr);
}
}
After dynamically allocating memory using kmalloc, theoretically, the maximum number of unsigned long long that can be computed is limited by the maximum length that kmalloc can allocate (128KB), which is equivalent to 2048 unsigned long long. The maximum number of decimal digits that can be represented is $\lfloor 2048*19.26593 + 1\rfloor=39457$.
For Fibonacci numbers with decimal digits less than or equal to 39457, the corresponding Fibonacci sequence index is given by $\lfloor k*0.20899 + 0.6505 \rfloor \leq 39457 \Rightarrow k \leq 188795$. Therefore, the current implementation can compute up to $F_{188795}$.
The implementation up to this point is in 0ee4f89 in ubig_2.h.
Introduce the Schönhage–Strassen Algorithm to Accelerate Multiplication
The concept of the Schönhage–Strassen Algorithm is to split the large numbers $x$ and $y$ into smaller numbers $x_0$, $x_1$, …, and $y_0$, $y_1$, … with $n$ digits each. Then, perform linear convolution on $(x_0, x_1, …)$ and $(y_0, y_1,…)$, and after completing the linear convolution, left-shift and add all elements according to their digits to achieve multiplication. For example:
Let $x = 26699$ and $y = 188$.
Splitting $x$ and $y$ into subsequences with 2 digits each yields the following sequences:
$(2, 66, 99),\ (1, 88)$
Perform linear convolution on these sequences:
1
2
3
4
5
6
7
2 66 99
x 1 88
-----------------------
176 5808 8712
2 66 99
-----------------------
2 242 5907 8712
The linear convolution of $(2, 66, 99)$ and $(1, 88)$ results in $(2, 242, 5907, 8712)$. Next, by left-shifting and adding the elements of the linear convolution, we can complete the multiplication of large numbers.
1
2
3
4
5
6
8712
5907
242
+ 2
--------------
5019412
In the multiplication implementation of ubig, I plan to split the numbers at the boundary of 32 bits and calculate the linear convolution using 64-bit multiplication. To facilitate the above operations, I am changing the data type of ubig from unsigned long long to unsigned int for storing the values.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
// find the array index of MSB of a
// TODO: use binary search
static inline int ubig_msb_idx(ubig *a)
{
int msb_i = a->size - 1;
while (msb_i >= 0 && !a->cell[msb_i])
msb_i--;
return msb_i;
}
void ubig_mul(ubig *dest, ubig *a, ubig *b)
{
zero_ubig(dest);
// find the array index of the MSB of a, b
int msb_a = ubig_msb_idx(a);
int msb_b = ubig_msb_idx(b);
// a == 0 or b == 0 then dest = 0
if (msb_a < 0 || msb_b < 0)
return;
// calculate the length of vector
// after doing linear convolution
// i.e. column number
int length = msb_a + msb_b + 1;
/* do linear convolution */
unsigned long long carry = 0;
for (int i = 0; i < length; i++) {
unsigned long long col_sum = carry;
carry = 0;
int end = (i <= msb_b) ? i : msb_b;
int start = i - end;
for (int j = start, k = end; j <= end; j++, k--) {
unsigned long long product =
(unsigned long long) a->cell[k] * b->cell[j];
col_sum += product;
carry += (col_sum < product);
}
dest->cell[i] = (unsigned int) col_sum;
carry = (carry << 32) + (col_sum >> 32);
}
dest->cell[length] = carry;
}
The complete implementation is in ubig_schonhange_strassen.h on commit b21a89a.
Introduce the Karatsuba Algorithm to Accelerate Multiplication
The concept of Karatsuba is to split $x$ and $y$ at the $n$th digit boundary into halves $x_1$, $x_0$, $y_1$, $y_0$, and consider them as smaller numbers to multiply. Then, compensate for the lost digits of $x_1$ and $y_1$ by left-shifting. Using decimal digits as an example:
\[\text{Let} \ x = x_1 * 10^n + x_0 \ \text{and} \ y = y_1 * 10^n + y_0\]Then, $x*y$ can be expressed as:
\[\underbrace{x_1y_1}_{z_2}*10^{2n}+\underbrace{(x_1y_0+y_1x_0)}_{z_1}*10^n+\underbrace{x_0y_0}_{z_0}\]The above algorithm for calculating $z_2$, $z_1$, and $z_0$ requires four multiplications. However, we can optimize it to three multiplications using the following technique:
By expanding $(x_1+x_0)(y_1+y_0)$, we get:
\[(x_1+x_0)(y_1+y_0)=\underbrace{x_1y_1}_{z_2}+\underbrace{x_1y_0+x_0y_1}_{z_1}+\underbrace{x_0y_0}_{z_0}\]After rearranging, we can calculate $z_1$ using $(x_1+x_0)(y_1+y_0)$, $z_0$, and $z_2$:
$z_2=x_1y_1$
$z_0 = x_0y_0$
$z_1=(x_1+x_0)(y_1+y_0)-z_0-z_2$
Finally, calculating $z_210^{2n}+z_110^n+z_0$ gives the result of $x$ multiplied by $y$.
The above is the Karatsuba algorithm.
Next, I will demonstrate Karatsuba using two 8-bit numbers to yield a 16-bit product (assuming the processor only supports 8-bit multiplication):
\[x = 01001001_2 = 73_{10}, \ y = 10000011_2 = 131_{10}\] \[x=x_110^4+x_0=010010^4+1001\] \[y=y_110^4+y_0=100010^4+0011\] \[z_2=x_1y_1=0100*1000=00100000\] \[z_0=x_0y_0=1001*0011=00011011\] \[z_1=(x_1+x_0)(y_1+y_0)-z_0-z_2\] \[\begin{align*} z_1 &=(x_1+x_0)(y_1+y_0)-z_0-z_2 \\ &=(0100+1001)(1000+0011)-00100000-00011011 \\ &=10001111-00100000-00011011 \\ &=01010100 \end{align*}\] \[\begin{align*} x*y &=z_2*10^8+z_1*10^4+z_0 \\ &=0010010101011011 \\ &=9563_{10} \end{align*}\]Where $*10^n$ can be replaced by left-shift operations.
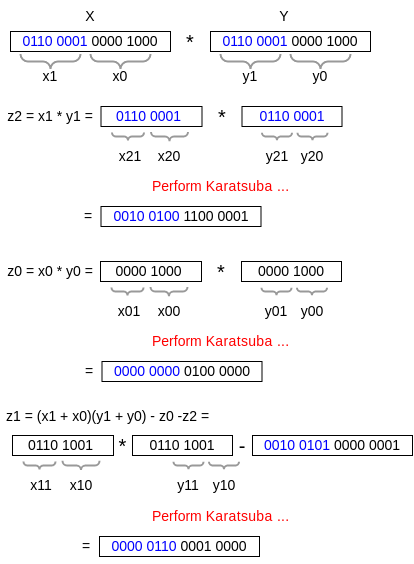
Continuing from the previous example, when $x$ and $y$ exceed 8 bits, Karatsuba can be implemented using a divide-and-conquer approach. If the number of bits in $x_1$, $x_0$, $y_1$, and $y_0$ exceeds the processor’s multiplication capacity, they can be further divided into $x_{11}$, $x_{10}$, $x_{01}$, $x_{00}$, etc., and Karatsuba can be applied again. Here’s a demonstration using two 16-bit numbers to yield a 32-bit product (assuming the processor only supports 8-bit multiplication):
The implementation of Karatsuba can be found in ubig_karatsuba.h at commit 9673a70.
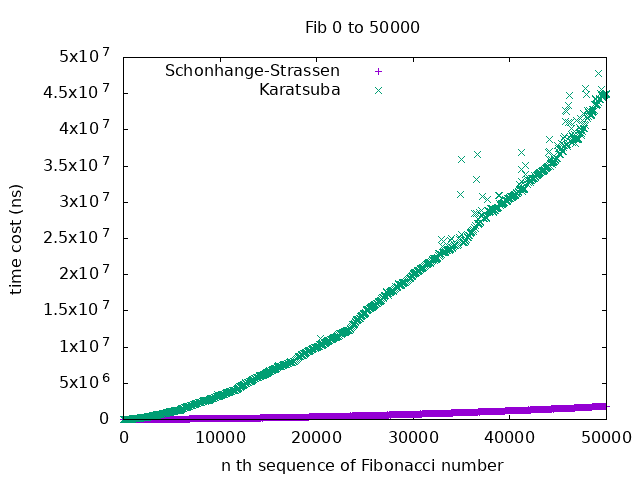
Comparing Karatsuba and Schönhage–Strassen Algorithms
The following chart displays the execution time for calculating $F_0$, $F_{50}$, $F_{100}$, …, $F_{50000}$ (excluding base conversion). The former takes around 45 milliseconds to calculate $F_{50000}$, while the latter takes approximately 1.8 milliseconds.
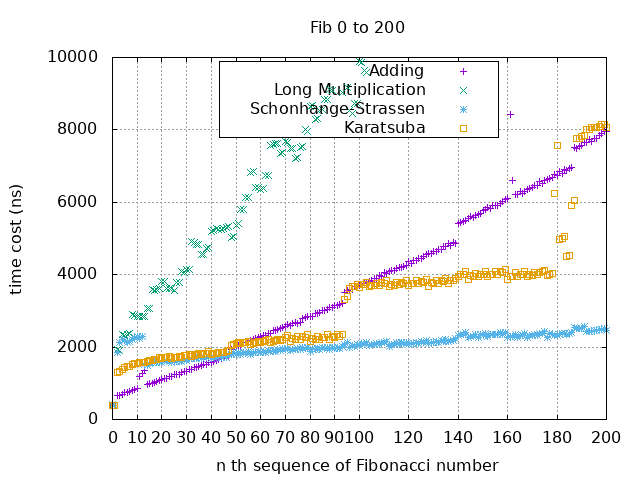
Next, let’s look at the time consumption of each algorithm when calculating smaller numbers:
From the chart, it can be observed that when calculating from $F_0$ to $F_{45}$, Adding is the fastest, while Karatsuba and Schönhage–Strassen are approximately equally fast from $F_{45}$ to $F_{95}$, and Schönhage–Strassen is the fastest for calculations beyond that.
Regarding the time complexity of the three algorithms for calculating $F_N$:
- Adding: It performs $N$ additions, with each addition requiring $log_{2^{32}}F_N$ iterations, resulting in a complexity of $O(N*log_{2^{32}}F_N)$.
- Long Multiplication (Fast Doubling): It requires $log_2N$ iterations, with each iteration’s long multiplication taking $O(log_2F_Nlog_{2^{32}}F_N)$, resulting in a complexity of $O(log_2Nlog_2F_N*log_{2^{32}}F_N)$.
- Schönhage–Strassen Fast Doubling: It also requires $log_2N$ iterations, with each iteration’s multiplication taking $O(1+2+…+log_{2^{32}}F_N+log_{2^{32}}F_N-1+…+2+1)=O(log_{2^{32}}F_Nlog_{2^{32}}F_N)$, resulting in a complexity of $O(log_2Nlog_{2^{32}}F_N*log_{2^{32}}F_N)$.

Comments powered by Disqus.