Exponential Golomb Coding

Exponential Golomb Coding

Excerpted from Wikipedia, Exponential-Golomb coding (or Exp-Golomb code) is a kind of Universal code, that is, Exp-Golomb code can be mapped to all positive integers.

Assuming the input is x, the encoding steps:

1. Write x + 1 in binary
2. Count the binary digit of the number x + 1 have in total, and add as many 0 as its binary digit minus 1 in front of x + 1.

Example 1:

x = 5
1. Write down 5 + 1 = 6 as binary "110".
2. "110" has 3 digits, we write 2 "0"s preceding "110".
   The Exp-Golomb code of 5 is "00110".

Example 2:

x = 24
1. Write down 24 + 1 = 25 as binary "11001".
2. "11001" has 5 digits, we write 4 "0"s preceding "11001".
   The Exp-Golomb code of 24 is "000011001".

Calculate the Exp-Golomb code of 0 ~ 8 according to the rules mentioned above:

 x   step 1   step 2
 0 ⇒  1     ⇒ 1
 1 ⇒  10    ⇒ 010
 2 ⇒  11    ⇒ 011
 3 ⇒  100   ⇒ 00100
 4 ⇒  101   ⇒ 00101
 5 ⇒  110   ⇒ 00110
 6 ⇒  111   ⇒ 00111
 7 ⇒  1000  ⇒ 0001000
 8 ⇒  1001  ⇒ 0001001

If you want to encode signed integers, just map each signed number to an unsigned number:

 x   map    step 1  step 2
 0 ⇒  0  ⇒  1     ⇒ 1
 1 ⇒  1  ⇒  10    ⇒ 010
−1 ⇒  2  ⇒  11    ⇒ 011
 2 ⇒  3  ⇒  100   ⇒ 00100
−2 ⇒  4  ⇒  101   ⇒ 00101
 3 ⇒  5  ⇒  110   ⇒ 00110
−3 ⇒  6  ⇒  111   ⇒ 00111
 4 ⇒  7  ⇒  1000  ⇒ 0001000
−4 ⇒  8  ⇒  1001  ⇒ 0001001

We can group every $2^i$ Exp-Golomb codes in order. For each code, there are $i$ 0s in front, which means that the code belongs to $S_i$. The red 1 in the center of each code is a dividing point, and the code of the suffix is expressed in binary as the $j$th element of $S_i$, recorded as $G_{i,j}$ :

$ \ S_0 \quad \quad \quad S_1 \quad \quad \quad \quad \quad \quad \quad \quad \ \ S_2 \\ \{\color{red}1\},\ \{0\color{red}10,\ 0\color{red}11\},\ \{00\color{red}100,\ 00\color{red}101,\ 00\color{red}110,\ 00\color{red}111\},\ … \\ G_{0,0} \ \ \ G_{1,0} \ \ \ G_{1,1} \quad \quad G_{2,0} \quad \ \ G_{2,1} \quad \ \ G_{2,2} \quad \ G_{2,3}$

Order-k Exponential Golomb Coding

Now, let’s generalize the encoding process of Exp-Golomb code. The number of 0 in the prefix, like aforementioned, represents which group the code is in. But there will be $2^{i+k}$ elements in each group, not ${2^i}$ as we mentioned. The suffix of each code is also lengthened by $k$ bits. This is called $k$ order Exp-Golomb code. The following shows how it looks like:

order-0

$ \ S_0 \quad \quad \quad S_1 \quad \quad \quad \quad \quad \quad \quad \quad \ \ S_2 \\ \{\color{red}1\},\ \{0\color{red}10,\ 0\color{red}11\},\ \{00\color{red}100,\ 00\color{red}101,\ 00\color{red}110,\ 00\color{red}111\},\ … \\ G_{0,0} \ \ \ G_{1,0} \ \ \ G_{1,1} \quad \quad G_{2,0} \quad \ \ G_{2,1} \quad \ \ G_{2,2} \quad \ G_{2,3}$

order-1

$ \ \quad S_0 \quad \quad \quad \quad \quad \quad \quad S_1 \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad S_2 \\ \{\color{red}10,\ \color{red}11\},\ \{0\color{red}100,\ 0\color{red}101,\ 0\color{red}110,\ 0\color{red}111\},\ \{00\color{red}1000,\ 00\color{red}1001,\ 00\color{red}1010,\ … \\ G_{0,0} \ \ G_{0,1} \quad \ G_{1,0} \quad G_{1,1} \quad G_{1,2} \quad G_{1,3} \quad \quad G_{3,0} \quad \quad \ G_{3,1} \quad \quad G_{3,2}$

order-2

$ \ \quad S_0 \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad S_1 \\ \{\color{red}100,\ \color{red}101,\ \color{red}110,\ \color{red}111\},\ \{0\color{red}1000,\ 0\color{red}1001,\ 0\color{red}1010,\ 0\color{red}1011,\ 0\color{red}1100,\ 0\color{red}1101,\ 0\color{red}1110,\ 0\color{red}1111\},\ …\\ G_{0,0} \ \ \ G_{0,1} \ \ G_{0,2} \ \ G_{0,3} \quad \ \ \ G_{1,0} \quad \ \ G_{1,1} \quad \ \ G_{1,2} \quad \ \ G_{1,3} \quad \ \ G_{1, 4} \quad \ \ G_{1, 5} \quad \ \ G_{1, 6} \quad \ G_{1, 7}$

the encoding steps of $k$ order Exp-Golomb code:

1. Write $x+2^k$ in binary
2. Count the binary digits the number $x+2^k$ have, denote as $b$
3. Put $b-k$ 0s in front of x + 1 in binary

x	order-0	order-1	order-2	order-3	order-4
0	1	10	100	1000	10000
1	010	11	101	1001	10001
2	011	0100	110	1010	10010
3	00100	0101	111	1011	10011
4	00101	0110	01000	1100	10100
5	00110	0111	01001	1101	10101
6	00111	001000	01010	1110	10110
7	0001000	001001	01011	1111	10111
8	0001001	001010	01100	010000	11000
9	0001010	001011	01101	010001	11001
10	0001011	001100	01110	010010	11010
11	0001100	001101	01111	010011	11011
12	0001101	001110	0010000	010100	11100

C Language Implementation

github repo: https://github.com/blueskyson/Exponential-Golomb-coding

First clone the repo and compile exp-golomb.c into encode, then link decode to encode:

$ gcc exp-golomb.c -o encode
$ ln -s encode decode

# Usage
encode [input file] [output file] [order-k]
decode [input file] [output file] [order-k]

# Example
./encode sample_text.txt text.encode 4
./decode text.encode text.decode 4

Main Program

This program can encode every uint8_t into exp-golomb code. In line 7 of the program, first set MAX_ORDER, which is the limit of order-k that the program can allow. The maximum limit of this program is order-31 because the code process uses 1 to 2 uint32_ts as the temporary buffer, if MAX_ORDER is greater than or equal to 32, it will cause the encoded data to span 3 uint32_t, I didn’t designed a corresponding mechanism to deal with it.

The BUFFER_SIZE macro determines the length of the buffer array. In the encode function, the buffer array is uint32_t buffer[BUFFER_SIZE]; in the decode function, the scratch array is uint8_t buffer[BUFFER_SIZE]. When the encoded/decoded data in buffer reach WRITE_SIZE, the data in the buffer will be written to the output file and the buffer will be emptied.

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <stdint.h>
#include <libgen.h>    //basename
#include <fcntl.h>     //open
#include <unistd.h>    //close
#include <sys/mman.h>  //mmap
#include <sys/stat.h>

#define MAX_ORDER 7    // must be smaller than 32
#define BUFFER_SIZE 100
#define WRITE_SIZE (BUFFER_SIZE - 2)

/* function status */
#define FAIL 0
#define SUCCESS 1

int encode(int, FILE*, int);
int decode(int, FILE*, int);

int main(int argc, char *argv[])
{
    if (argc < 3) {
        puts("Usage:\n"
             "encode [input file] [output file] [order-k]\n"
             "decode [input file] [output file] [order-k]");
        return 0;
    }
    
    /* open argv[1] as input file */
    int in_fd = open(argv[1], O_RDONLY);
    if (in_fd < 0) {
        puts("cannot open input file");
        return 0;
    }

    /* open argv[2] as output file */
    FILE *out_file = fopen(argv[2], "wb");
    if (!out_file) {
        puts("cannot open output file");
        return 0; 
    }

    /* read argv[3] as order */
    long int order = 0;
    if (argc >= 4) {
        char* endptr;
        order = strtol(argv[3], &endptr, 10);
        if (endptr == argv[3]) {
            puts("order is not a decimal number");
            return 0;
        }

        if (order > MAX_ORDER) {
            puts("order larger than max order");
            return 0;
        }
    }

    int status;
    if (strcmp(basename(argv[0]), "encode") == 0) {
        status = encode(in_fd, out_file, order);
    } else {
        status = decode(in_fd, out_file, order);
    }

    fclose(out_file);
    close(in_fd);
    if (status == FAIL) {
        remove(argv[2]);
    }

    return 0;
}

Encode

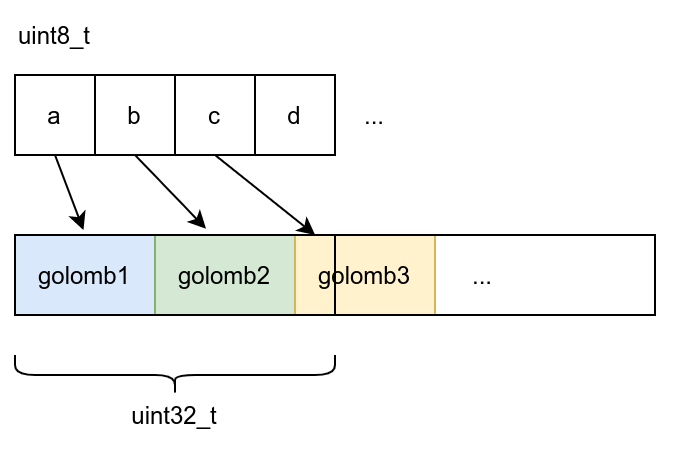
Use mmap to open the input file as uint8_t*. The converted exp-golomb code will be tightly arranged in the uint32_t array, as shown below:

The encoding method used here is the same as mentioned:

1. Write $x+2^k$ in binary
2. Count the binary digits the number $x+2^k$ have, denote as $b$
3. Put $b-k$ 0s in front of x + 1 in binary

After converting all the data, add a (uint32_t) 1 as a mark to end the file.

int encode(int in_fd, FILE* out_file, int order)
{
    struct stat s;
    if (fstat(in_fd, &s) < 0) {
        puts("cannot get status of iniput file");
        return FAIL;
    }
    
    uint8_t *map = (uint8_t*) mmap(0, s.st_size, PROT_READ, MAP_PRIVATE, in_fd, 0);
    if (map == MAP_FAILED) {
        puts("cannot open mmap");
        return FAIL;
    }
    
    uint32_t buffer[BUFFER_SIZE];
    memset(buffer, 0, sizeof(buffer));
    int buffer_index = 0;
    int cursor = 32;
    uint32_t offset = 1 << order;

    /* start to encode */
    for (long int i = 0; i < s.st_size; i++) {
        uint32_t current = (uint32_t) map[i];
        current += offset;
        int clz = __builtin_clz(current);
        int unary_width = 31 - clz - order;
        int binary_width = 32 - clz;
        
        /* write unary */
        cursor -= unary_width;
        if (cursor <= 0) {
            cursor += 32;
            buffer_index++;
        }
        
        /* write binary */
        if (cursor < binary_width) {    // truncate in uint32_t
            buffer[buffer_index++] |= current >> (binary_width - cursor);
            buffer[buffer_index] |= current << (32 - (binary_width - cursor));
            cursor = cursor + 32 - binary_width;
        } else {
            buffer[buffer_index] |= current << (cursor - binary_width);
            cursor -= binary_width;
        }

        /* write buffer */
        if (buffer_index >= WRITE_SIZE) {
            fwrite(buffer, 4, WRITE_SIZE, out_file);
            uint32_t tail = buffer[buffer_index];
            memset(buffer, 0, sizeof(buffer));
            buffer[0] = tail;
            buffer_index = 0;
        }
    }

    /* finalize */
    buffer[buffer_index + 1] = (uint32_t) 1; //end signal
    fwrite(buffer, 4, buffer_index + 2, out_file);
    return SUCCESS;
}

Decode

Here we reverse the steps of encoding. The only thing to note is that [-Wshift-count-overflow] will occur when uint32_t is shifted left or right by 32 bits, so an if-condition is in line 58 to avoid shifting 32 bits.

int decode(int in_fd, FILE* out_file, int order)
{
    struct stat s;
    if (fstat(in_fd, &s) < 0) {
        puts("cannot get status of iniput file");
        return FAIL;
    }
    
    uint32_t *map = (uint32_t*) mmap(0, s.st_size, PROT_READ, MAP_PRIVATE, in_fd, 0);
    if (map == MAP_FAILED) {
        puts("cannot open mmap");
        return FAIL;
    }

    uint8_t buffer[BUFFER_SIZE];
    memset(buffer, 0, sizeof(buffer));
    int buffer_index = 0;
    int cursor = 32;
    uint32_t offset = 1 << order;
    int map_index = 0;
    uint32_t current = map[0];
    
    while (1) {
        /* read unary */
        int unary_width = 0;
        if (current == 0) {             // truncate in unary field
            current = map[++map_index];
            int clz = __builtin_clz(current);
            unary_width = cursor + clz;
            cursor = 32 - clz;
        } else {
            int clz = __builtin_clz(current);
            unary_width = clz - (32 - cursor);
            cursor = 32 - clz;
        }

        /* end of file is (uint32_t) 1 ,
         * the leading zero of end of file is 31 */
        if (unary_width >= 31) {
            break;
        }

        /* read binary */
        int binary_width = unary_width + 1 + order; 
        uint32_t tmp = 0;
        if (binary_width > cursor) {    // truncate in binary field
            tmp = current << (binary_width - cursor);
            current = map[++map_index];
            binary_width -= cursor;
            cursor = 32;
        }

        tmp |= current >> (cursor - binary_width);
        tmp -= offset;
        buffer[buffer_index++] = (uint8_t) tmp;
        
        /* be careful for left shift 32 bits */
        cursor -= binary_width;
        if (cursor == 0) {
            current = 0;
        } else {
            int shift = 32 - cursor;
            current = (current << shift) >> shift;
        }
        
        if (buffer_index == BUFFER_SIZE) {
            fwrite(buffer, 1, BUFFER_SIZE, out_file);
            buffer_index = 0;
        }
    }

    /* finalize */
    if (buffer_index != 0) {
        fwrite(buffer, 1, buffer_index, out_file);
    }

    return SUCCESS;
}

Bit Width of Exponential Golomb Coding

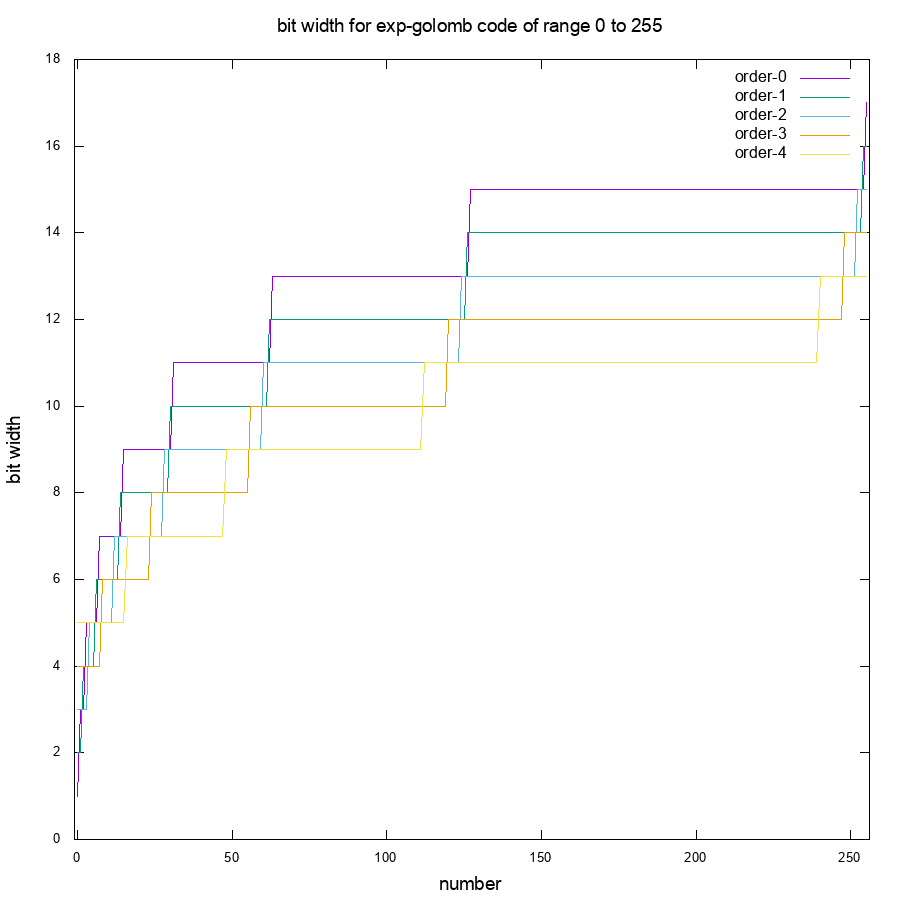
The figure below shows the bit length occupied by the 8-bit value after encoding from order 0 to 4. It can be seen that except for order-4, other exp-golomb codes reach the length of 8 bits before the original value is greater than 50. However, the commonly used numbers and English letters in ASCII code are between ‘0’ (48) and ‘z’ (122), which exceed 50 characters and make the exp-golomb code exceed 8 bits. One should implement other strategy with exp-golomb code to compress data.