Arrange these functions under the Big-$O$ notation in increasing order of growth rate with $g(n)$ following $f(n)$ in your list if and only if $f(n) = O(g(n))$ (here, $log(x)$ is the natural logarithm of $x$, with the base being the Euler’s number $e$): \(\sqrt{n}^{\sqrt{n}}, n^{\log n}, n \log(\log n), n^{\frac{1}{\log n}}, 2^{\log n}, \log^2 n, (\log n)^{\sqrt{\log n}}.\)
Solution:
First, we can simplify some functions such as $n^{\frac{1}{\log n}} = n^{\frac{\log 2}{\log n}} = n^{\log_n2} = 2$, and $2^{\log n} = n.$
Second, we apply a $\log$ to every function for an easier comparison:
\[\begin{aligned} & \log{\sqrt{n}^{\sqrt{n}}} = \sqrt{n}\log{\sqrt{n}} = \frac{\sqrt{n}}{2}\log n, & \log{n^{\log n}} = \log n \log n, \\ & \log{(n \log(\log n))} = \log n + \log \log \log n, & \log{2}, \\ & \log{n}, & \log{(\log^2 n)} = 2 \log \log n, \\ & \log{((\log n)^{\sqrt{\log n}})} = \sqrt{\log n} \log \log n \end{aligned}\]Based on the above, the increasing order of grow rate is: \(O(n^{\frac{1}{\log n}}) ≤ O(\log^2 n) ≤ O((\log n)^{\sqrt{\log n}}) ≤ O(2^{\log n}) ≤ O(n\log(\log n)) ≤ O(n^{\log n}) ≤ O(\sqrt{n}^{\sqrt{n}})\)
The Fibonacci sequence $F_1, F_2, F_3, …$, is defined as follows. $F_1 = F_2 = 1$ and $F_n = F_{n−1} + F_{n−2}$ for $n ≥ 3$. For example, $F_3 = F_2 + F_1 = 2$ and $F_4 = F_3 + F_2 = 3$. Prove by induction that $F_{n+2} = 1 + \sum_{i=1}^{n}{F_i}$ for $n ≥ 1$.
Solution:
BC: $n=1, F_{1+2} = 1 + \sum_{i=1}^{1}F_i = 1 + 1 = 2$ which complies with $F_3 = F_2 + F_1 = 2.$ Verified.
IH: Assume $F_{n+2} = 1 + \sum_{i=1}^{n}F_i$ holds with $n = k$.
IS: Prove $F_{n+2} = 1 + \sum_{i=1}^{n}F_i$ holds with $n = k + 1$.
Left hand side: $F_{(k+1) + 2} = F_{k + 3} = F_{k+2} + F_{k+1}$.
Right hand side: $1 + \sum_{i=1}^{k+1}F_i = (1 + \sum_{i=1}^{k}F_i) + F_{k+1} = F_{k+2} + F_{k+1}$.
Left hand side equals to right hand side. Thus, the given statement is true.
Given a connected graph $G = (V, E)$ and a specific vertex $u ∈ V$. Suppose we compute a DFS tree rooted at $u$, and obtain a tree $T$ that includes all nodes of $G$. Suppose we then compute a BFS tree rooted at $u$, and obtain the same tree $T$. Prove by contradiction that $G$ has the same structure as $T$, that is, $G$ cannot contain any edges that do not belong to $T$.
Hint: You can use the fact that if $T$ is a BFS tree of $G = (V, E)$ and $(x, y) ∈ E$, then in $T$ the levels of $x$ and $y$ differ by at most $1$.
Solution:
Assume there’s an edge $(x, y)∈E$ but not in $T$. Then $x$ and $y$ must:
(a) Connect two vertices on the same branch with a level difference greater than $1$.
(b) Be on different branches of $T$.
However, in either case (a) or (b), BFS and DFS don’t generate the same $T$ structure when such an edge exists. Also, the existence of edge connecting vertices with a level difference greater than $1$ contradicts the truth that the levels of $x$ and $y$ differ by at most $1$ in BFS trees. It follows that $G$ cannot contain any edges that do not belong to $T$.
Given an unweighted, undirected, and connected graph $G = (V, E)$. Construct an algorithm to determine maximum of the shortest-path distances between all pairs of nodes in $G$ (also called the diameter of the graph). Also, determine the time complexity of your algorithm and justify your answer.
Solution:
Run BFS from each node as the source. Update the max distance that BFS reached in each run. Return the max distance as the diameter of the graph. The time complexity is $O(\lvert V \rvert*(\lvert V \rvert + \lvert E \rvert))$. Pseudocode:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
int findDiameter(G):
maxDistance = 0
foreach node n in G:
distance = BFS(n, G)
maxDistance = max(maxDistance, distance)
return maxDistance
int BFS(source, G):
foreach node n in G:
distances[n] = INT32_MIN
distances[source] = 0
maxDistance = 0
Q = queue()
Q.enqueue(source)
while !Q.empty():
v = Q.dequeue()
for w in neighbors of v:
if distances[w] == INT32_MIN:
distances[w] = distances[v] + 1
Q.enqueue(w)
maxDistance = max(maxDistance, distances[w])
return maxDistance
Given an unweighted and undirected graph $G = (V, E)$ and an edge $e ∈ E$. Construct an algorithm to determine whether the graph $G$ has a cycle containing that specific given edge $e$. Also, determine the time complexity of your algorithm and justify your answer.
Note: To become eligible for full credits on this problem, the running time of your algorithm should be bounded by $O(\lvert V \rvert + \lvert E \rvert)$.
Solution:
Denote nodes form $e$ as $x$ and $y$, i.e. $e=(x,y)$. We choose $x$ as the source and then perform BFS without traversing $e$. If we find a route reaching $y$, we prove there is a cycle. The time complexity is the same as pure BFS’s, bounded by $O(\lvert V \rvert + \lvert E \rvert)$. Pseudocode:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
bool detectCycle(G, e):
x, y = e[0], e[1]
Remove y from neighbors of x // Exclude edge e
foreach node n in G:
visited[n] = false
visited[x] = true
Q = queue()
Q.enqueue(x)
while !Q.empty():
v = Q.dequeue()
for w in neighbors of v:
if w == y: // If we find y, the cycle containing e is detected
Add y back to neighbors of x
return true
if !visited[w]:
visited[w] = true
Q.enqueue(w)
return false
A directed graph $G = (V, E)$ is singly connected if $u⇝v$ implies that $G$ contains at most one simple path from $u$ to $v$ for all vertices $u, v ∈ V$. Construct an algorithm to determine whether or not a directed graph is singly connected. Also, determine the time complexity of your algorithm and justify your answer.
Solution:
Run DFS from each node in the graph as the source. Track the visit count of each node during the traversal. If the source node is visited $3$ times (counting the DFS initialization as $1$), or any other node is visited $2$ times, we found $2$ paths from the source to the node. Thus, the graph is determined to not be singly connected. Otherwise, the graph is singly connected if we can’t visit the source node for $3$ times or any other node for $2$ times.The time complexity is $O(\lvert V \rvert *(\lvert V \rvert + \lvert E \rvert))$. Pseudocode:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
bool isSinglyConnected(G):
foreach node n in G:
for i = 0 to n:
visitCount[n] = 0
DFS(n, n, visitCount, G):
visitCount[n] -= 1;
for i = 0 to n:
if visitCount[i] >= 2:
return false
return true
bool DFS(source, v, visitCount, G):
visitCount[v] += 1
for w in neighbors of v:
if visitCount[w] > 0:
visitCount[w] += 1
else:
DFS(source, w, visitCount, G):
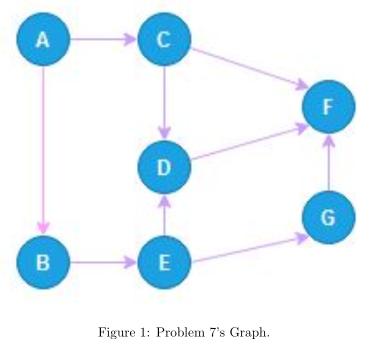
According to the Topological Sort for DAG described in Lecture 1, given the graph below
(a) Please find one possible topological order of the graph in Figure 1.
(b) In addition, could you find all the possible topological orders?
Solution:
(a) A→B→C→E→D→G→F
(b) Based on backtracking combined with Kahn’s algorithm, 7 orders were found.
Given a sequence of $n$ operations, suppose the $i$-th operation cost $i + j$ if $i = 2^j$ for some integer $j$; otherwise, the cost is $1$. Prove that the amortized cost per operation is $O(1)$.
Solution:
Consider we execute from $i = 1$ to $i = 2^k$ operations. The total cost is
\[\begin{aligned} & \underbrace{(1 + 1 + 1 + \ldots + 1)}_\text{operations that cost 1} + \underbrace{(2^0+2^1+2^2+ \ldots +2^k)}_{i\text{ part of operations that cost }i+j}+\underbrace{(0 + 1 + 2 + \ldots + k)}_{j\text{ part of operations that cost }i + j} \\ & = (2^k - k) + (2^{k+1}-1)+\frac{k(k+1)}{2} \\ & = 3*2^k+\frac{k^2}{2}-\frac{k}{2}+1 \\ \end{aligned}\] \[\text{Amortized Cost}=\lim_{k→∞}\frac{3*2^k+\frac{k^2}{2}-\frac{k}{2}+1}{2^k}=3=O(1)\]Suppose we perform a sequence of stack operations on a stack whose size never exceeds $k$. After every $k$ operations, we make a copy of the entire stack for backup purposes. Show that the cost of $n$ stack operations, including copying the stack, is $O(n)$ by assigning suitable amortized costs to the various stack operations.
Solution:
Assign $2$ credits to PUSH, spend $1$ for push operation itself and save $1$ for future backup.
Assign $2$ credits to POP, spend $1$ for pop operation itself and save $1$ for future backup.
When we reach $k$ operations, we have $k$ credits in the bank to make a copy of the entire stack where size ≤ $k$.
Since both amortized costs of PUSH and POP are $O(1)$, the totcal cost of $n$ operations is $O(n)$.
In a data structure, there is a doubly linked list with ‘head’ and ‘tail’ pointers for storing $n$ elements. When searching for a specific element, the search starts from the head and proceeds until the target element is found, at an index $i$ where $i ≤ n$. The cost for each ‘search’ operation is $i$, and when the target element is found, it’s moved towards the head of the list by $1$ index at a cost of $c$ (a positive constant). We want to calculate the amortized time complexity for searching and moving an element in the worst-case scenario. Assume that the number of times the target element is searched is less than or equal to the total number of elements in the list, and consider a scenario where we search for this specific element repeatedly.
Solution:
The worst-case is to search the $n$-th element. The cost for searching and moving an $n$-th element is $n + c$. After the first search, the element is in the $n-1$-th position, so the cost reduce $1$ when searching the same element. After doing so for $n$ times, the element is in the $1$-st position and the cost become $1+c$. (The cost may be $1$ without the redundant move cost $c$. It depends on implementation.)
The total cost of worst-case searching a specific element for $n$ times is
\[(n + c) + (n - 1 + c) + ... + (1 + c) =\frac{n(n+1)}{2}+cn =\frac{n^2}{2}+n(c+\frac{1}{2})\] \[\text{Amortized Cost}=\lim_{n→∞}\frac{\frac{n^2}{2}+n(c+\frac{1}{2})}{n}=\frac{n}{2} + c=O(n)\]
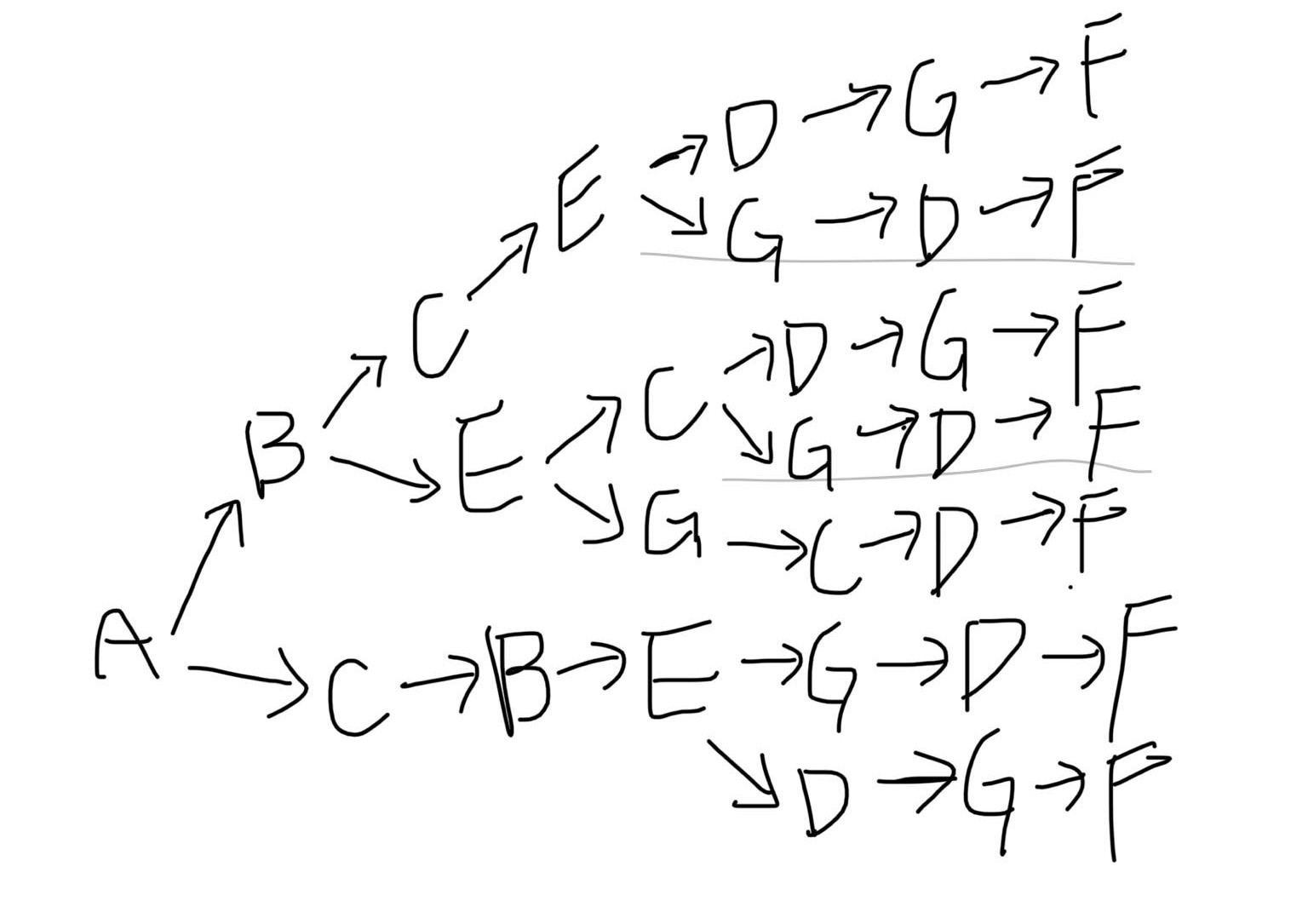
Comments powered by Disqus.